HIGH PRESSURE AFFECTION ON RATES OF MONOMOLECULAR THERMAL DECOMPOSITION OF O-NITROARYLAZIDES IN SOLUTIONS
Yury M. Burov*, Boris S. Fedorov*, Vladimir A. Charskii*, Olga V. Kovalchukova **
*- Institute of the Problems of Chemical Physics, RAS, Chernogolovka , Russia
**- Peoples' Friendship University of Russia
The kinetics of reactions in dense media exhibits a number of specific features in comparison with the kinetics of gas-phase reactions. For example, formation of an activated complex is accompanied by changes in shape and size of a molecule, and, therefore, the neighboring molecules may impede this process. At a macroscopic level, this effect manifests itself as dependences of the reaction rate constant k on pressure, aggregate state of a substance, and characteristics of polymorphous transitions, i.e. on density of the medium. While studying the processes of detonation and thermal decomposition of energetic materials in a solid state, these phenomena should be taken into consideration.
Traditionally, this problem has been treated within the framework of Evans – Polanya theory [1], which was first stated by van't Hoff [2] in the following way: when the activated complex is formed, the initial volume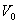 
of the molecule changes by the value of the activation volume 
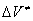. To cause the corresponding deformation in the surrounding medium, it is necessary to spend an additional energy of 
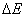, the value by which the activation energy E increases. The pressure dependence of the rate constant for reactions in liquid media is given by [1]
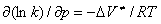, (1)
where p is the external pressure and R is the universal gas constant.
A similar expression was derived for reactions in crystals [3]. In this case, the additional energy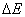 
equals the energy of elastic deformation of the crystal by a value of 
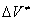; i.e.,
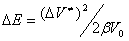, (2)
where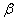 
is the compressibility of the substance.
In this approach, the substance is considered as a continuous medium, with the only property of interest being its ability to transmit external pressure. Such a medium resembles Maxwell's ether. In spite of the fact, that the theory of Evans – Polanya contradicts the experiment, it exists without any principle changes for more than 100 years.
This problem was analyzed in [4]. It was shown that an elementary act of a chemical reaction in dense media can not be described in frames of the equilibrium thermodynamics. A simple model of a monomolecular reaction in a dense medium was developed. In this model, the rate of a chemical reaction with a positive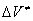 
is determined by existence of free volume in the substance. The proposed model is in a good agreement with the experiment. For reactions with a negative 
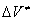the parabolic-like dependence of the rate constant on pressure.
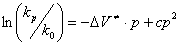(3)
The above experiment was performed to prove experimentally this these.
In performing of a such investigation, the choice of an investigated object is of a special importance. The tested reaction should be a simple one, so that no problems with interpretation of its mechanism arise. It should not be complicated by site processes. The reaction of thermal decomposition of o-nitroarylazides is up to the above requirements.
As it was shown, the thermal decomposition of o-nitroarylazides passes via a cyclic intermediate state [5]. It is followed by formation of a corresponding furoxane and detachment of one nitrogen molecule at the same time. One can suppose that the activation volume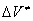 
of this reaction is either close to zero or negative. We investigated the affection of crystalline state on the rate of a monomolecular reaction with a small or negative activation volume.
For this purpose, we examined trinitro-triazido-benzene (I), m.p. 131 o C decomposition of which can be studied in a solid state, as well as ortho-nitroazido-benzene (II) which is the simplest representative of substances of this class.
The activation volume was detected by affection of high pressure on rates of decomposition of I and II in benzene solutions. The kinetics of the reaction in the solution was studied by the method of liquid-gas chromatography using the decrease of the reactant. The rate constants in solutions were measured at 80 o C.
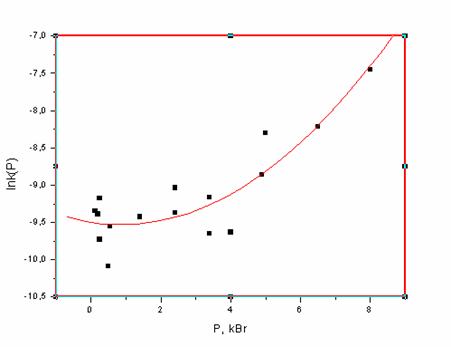
Fig. 1. The dependence of rate constants of thermal decomposition of I on perssure.
We found out that the rate of the reaction in the solution is related to the equation of the 1-st order. The rate constants measured both by yield of nitrogen or decay of the reactant was found to be the same. The rate of decomposition of I under atmospheric pressure is 4.5 times higher that the one of II. It is close to the value of a statistic factor of the reaction, s =3. That indicates the stepwise mechanism of decomposition of I.
In whole, high pressure accelerates the decomposition of both I and II. The dependence may be described for I as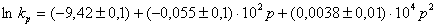 
,
And for II as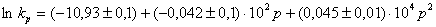 
,
where P (Pa) is the external pressure.
The activation volumes calculated through a linear term, are found to be 2.1 cm 3 ? mole –1 for I and 1.6 cm 3 ? mole –1 for II. These values are rather small. One can consider then that in frames of the error of the experiment they equal zero.
The decomposition of I in a solid state was studied by a manometric method in the temperature interval from 70 to 130 o C. In the temperature interval 70 – 100 o C the temperature dependence of rate constants is described by Arrhenius' equation with the following parameters: Ea = 28.8 kCal ? mole –1 , logA = 12.2 s –1 . At 80 o C the reterded effect of a lattice k l /k s = 44.2.
Thus, despite a small, practically zero-volume of activation, which accelerates in whole the affection of a high pressure on a rate constant, the retarded effect of a lattice of trinitro-triazido-benzene does not differ significantly from other organic substances with similar melting points. This may indicate that the existing ideas about existing of an activation volume in a crystal need to be revised. Apparently, for a reaction proceeds in a lattice, it is in need of some free volume which makes the molecule free enough, “liquid-like”. This volume does not depend on the type of the reaction, but it is determined by the dimensions of the cell which contains the molecule, just as to melt a crystal, a volume of about 10 per cent of a molar volume is in need.
REFERENCES
[1] M.G. Evans and M. Polanya, . 31 , p. 875, 1935. Trans. Faraday Soc
[2] J.H.van't Hoff, Lectures on Theoretical and Physical Chemistry (F.
Vieweg und Sohn, Braunschweig, 1898-1900.
[3] G. B. Manelis, Problems of Kinetics of Elementary Chemical Reactions
(Nauka, Moscow, 1973), p. 93 [in Russian].
[4] Yu. M. Burov, Russian Journal of Physical Chemistry, Vol. 78, No. 4, p. 579, 2004.
[5] S. Pata, Y. Gotstal, J. Chem. Soc., B, p. 489, 1966.
